Cosine+Spikes in Dirac-Cosine Basis

The Cosine+Spikes signal in this example consists of a mixture of 3 different cosine waves with different amplitudes and 120 different spikes (with normally distributed amplitudes and randomly chosen locations).

The Cosine part of the signal has a sparse representation in the Cosine (DCT) basis. The Spikes part of the signal has a sparse representation in the Dirac(Identity/Standard) basis. Thus, the mixture Cosine+Spikes signal has a sparse representation (of 123 nonzero coefficients) in the Dirac-Cosine two ortho basis.

Note that the spikes are normally distributed. Some of the spikes have extremely low amplitudes. They may be missed by a recovery algorithm depending on convergence thresholds.

See also:

• Test Problems

• Linear Operators

# Configure JAX to work with 64-bit floating point precision.
from jax.config import config
config.update("jax_enable_x64", True)

import jax.numpy as jnp
import cr.nimble as crn
import cr.sparse.plots as crplot

Setup

We shall construct our test signal and dictionary using our test problems module.

from cr.sparse import problems
prob = problems.generate('cosine-spikes:dirac-dct', c=3)
fig, ax = problems.plot(prob)

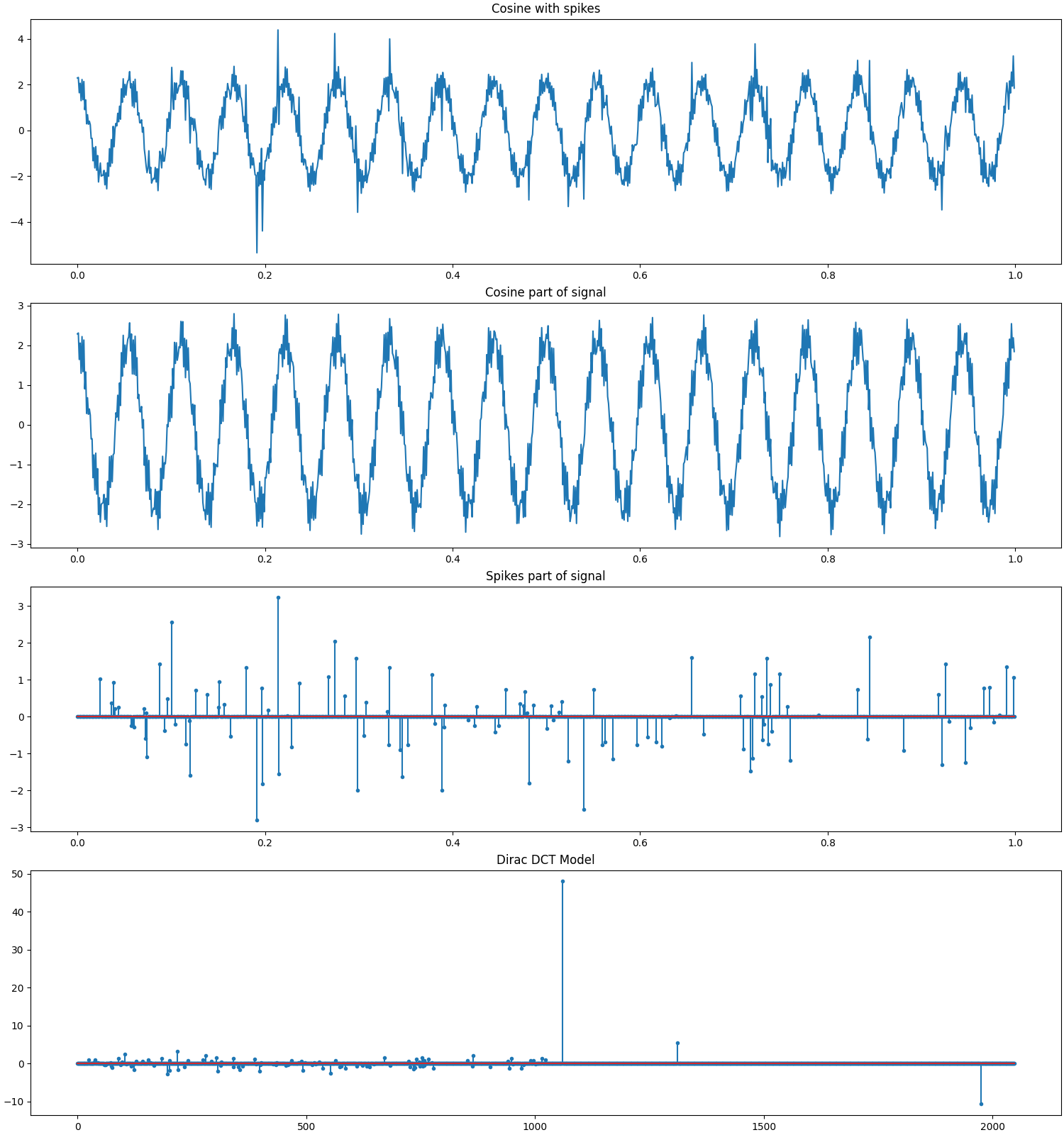
Let us access the relevant parts of our test problem

# The sparsifying basis linear operator
A = prob.A
# The Cosine+Spikes signal
b0 = prob.b
# The sparse representation of the signal in the dictionary
x0 = prob.x

Check how many coefficients in the sparse representation are sufficient to capture 99.9% of the energy of the signal

print(crn.num_largest_coeffs_for_energy_percent(x0, 99.9))

78

This number gives us an idea about the required sparsity to be configured for greedy pursuit algorithms.

Sparse Recovery using Subspace Pursuit

We shall use subspace pursuit to reconstruct the signal.

import cr.sparse.pursuit.sp as sp

# We will first try to estimate a 100-sparse representation
sol = sp.solve(A, b0, 100)

This utility function helps us quickly analyze the quality of reconstruction

problems.analyze_solution(prob, sol)

m: 1024, n: 2048
b_norm: original: 50.698 reconstruction: 50.695 SNR: 38.38 dB
x_norm: original: 50.704 reconstruction: 50.673 SNR: 38.36 dB
Sparsity: original: 78, reconstructed: 76, overlap: 76, ratio: 0.974
Iterations: 20

It takes 20 iterations to converge and 76 of the largest 78 entries have been correctly identified.

We will now try to estimate a 150-sparse representation

sol = sp.solve(A, b0, 150)
problems.analyze_solution(prob, sol)

m: 1024, n: 2048
b_norm: original: 50.698 reconstruction: 50.698 SNR: 294.28 dB
x_norm: original: 50.704 reconstruction: 50.704 SNR: 294.33 dB
Sparsity: original: 78, reconstructed: 78, overlap: 78, ratio: 1.000
Iterations: 5

We have correctly detected all the 78 most significant entries Let us check if we correctly decoded all the nonzero entries in the sparse representation x

problems.analyze_solution(prob, sol, perc=100)

m: 1024, n: 2048
b_norm: original: 50.698 reconstruction: 50.698 SNR: 294.28 dB
x_norm: original: 50.704 reconstruction: 50.704 SNR: 294.33 dB
Sparsity: original: 123, reconstructed: 123, overlap: 123, ratio: 1.000
Iterations: 5

The estimated sparse representation

x = sol.x

Let us reconstruct the signal from this sparse representation

b = prob.reconstruct(x)

Let us visualize the original and reconstructed representation

ax = crplot.h_plots(2)
ax[0].stem(x0, markerfmt='.')
ax[1].stem(x, markerfmt='.')

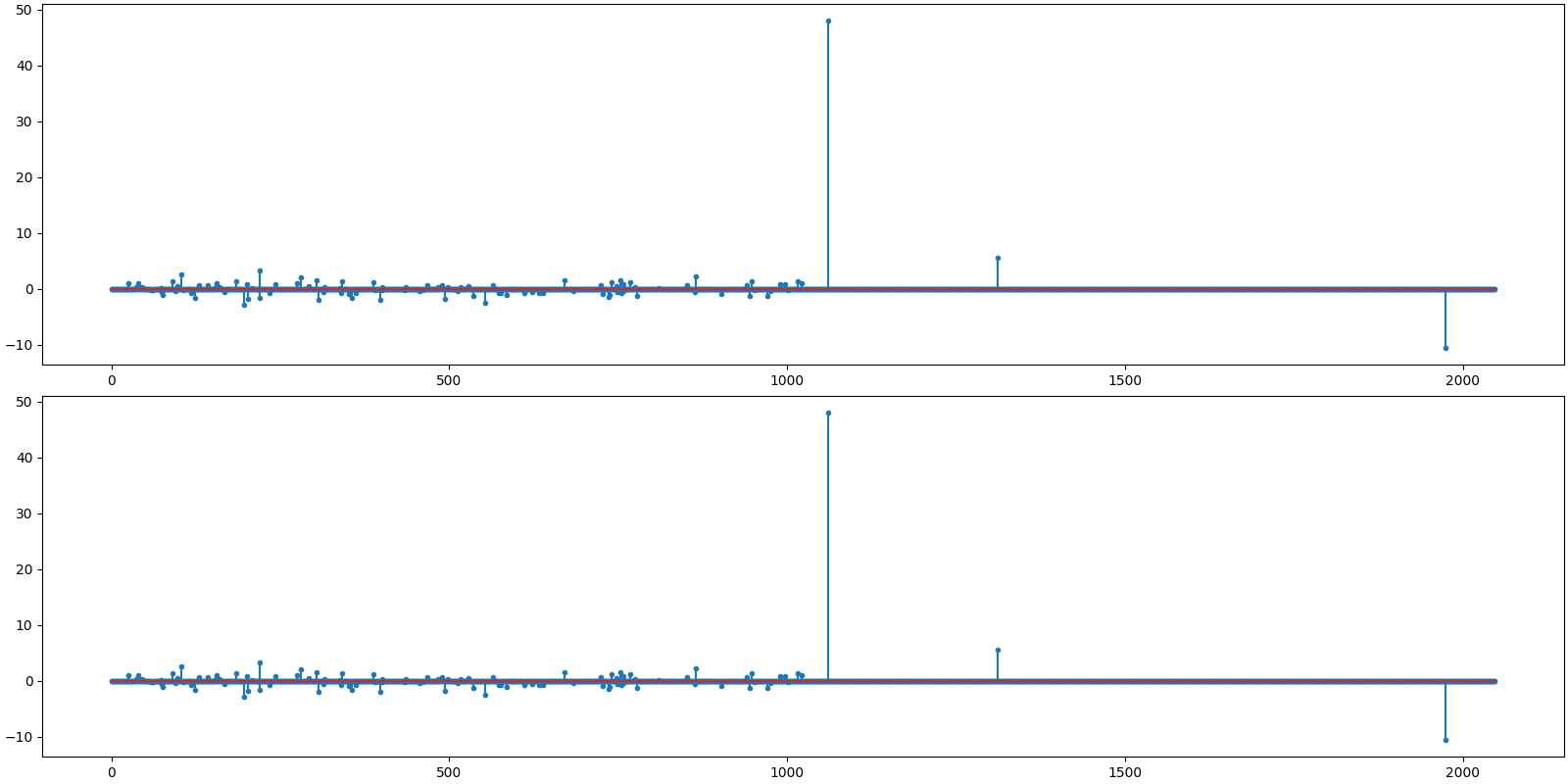
<StemContainer object of 3 artists>

Let us visualize the original and reconstructed signal

ax = crplot.h_plots(2)
ax[0].plot(b0)
ax[1].plot(b)

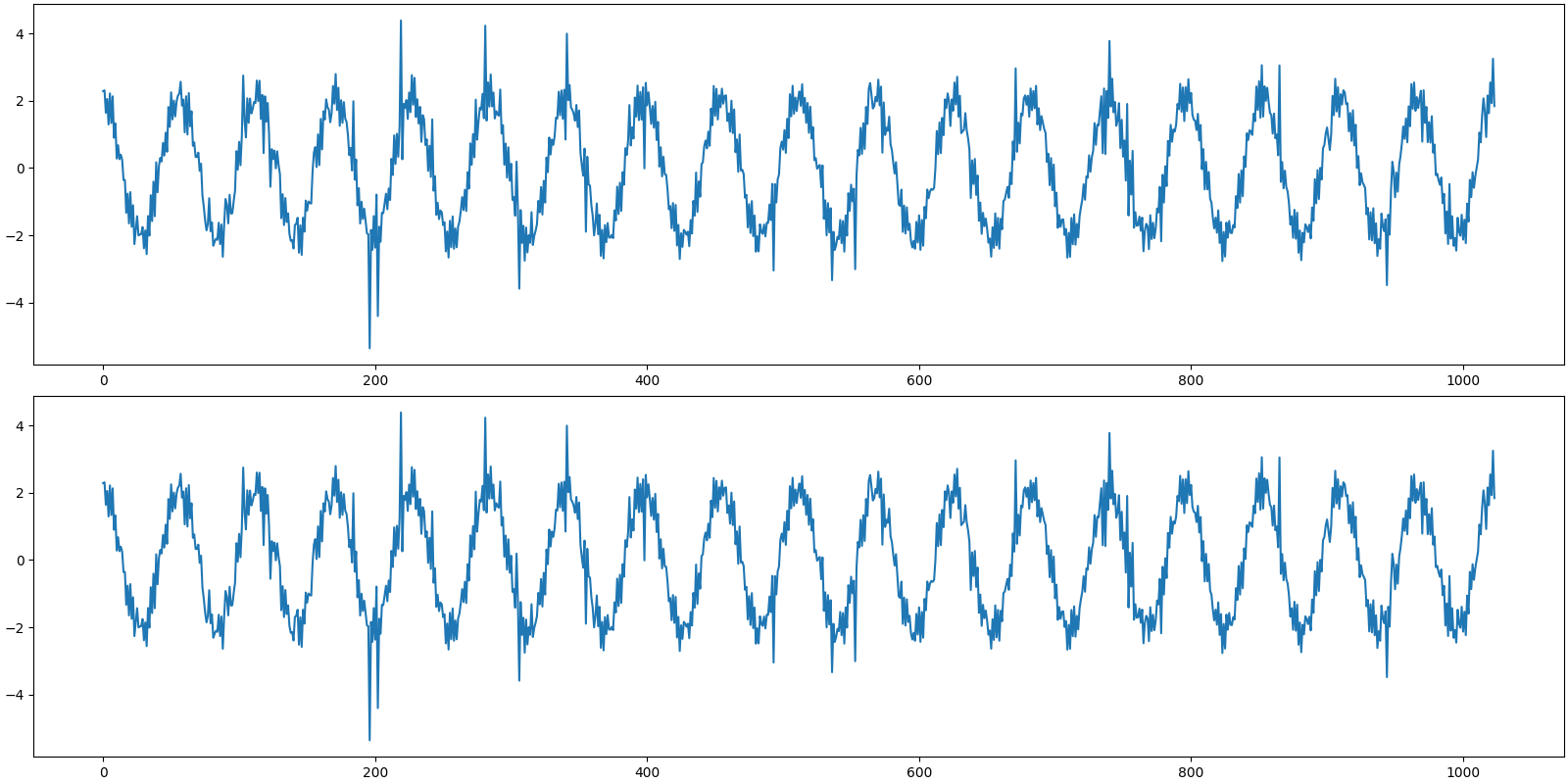
[<matplotlib.lines.Line2D object at 0x7f200c947f10>]

Sparse Recovery using Compressive Sampling Matching Pursuit

We shall now use compressive sampling matching pursuit to reconstruct the signal.

import cr.sparse.pursuit.cosamp as cosamp
# We will try to estimate a 150-sparse representation
sol = cosamp.solve(A, b0, 150)
problems.analyze_solution(prob, sol, perc=100)

m: 1024, n: 2048
b_norm: original: 50.698 reconstruction: 50.698 SNR: 296.28 dB
x_norm: original: 50.704 reconstruction: 50.704 SNR: 295.75 dB
Sparsity: original: 123, reconstructed: 123, overlap: 123, ratio: 1.000
Iterations: 6

The estimated sparse representation

x = sol.x

Let us reconstruct the signal from this sparse representation

b = prob.reconstruct(x)

Let us visualize the original and reconstructed representation

ax = crplot.h_plots(2)
ax[0].stem(x0, markerfmt='.')
ax[1].stem(x, markerfmt='.')

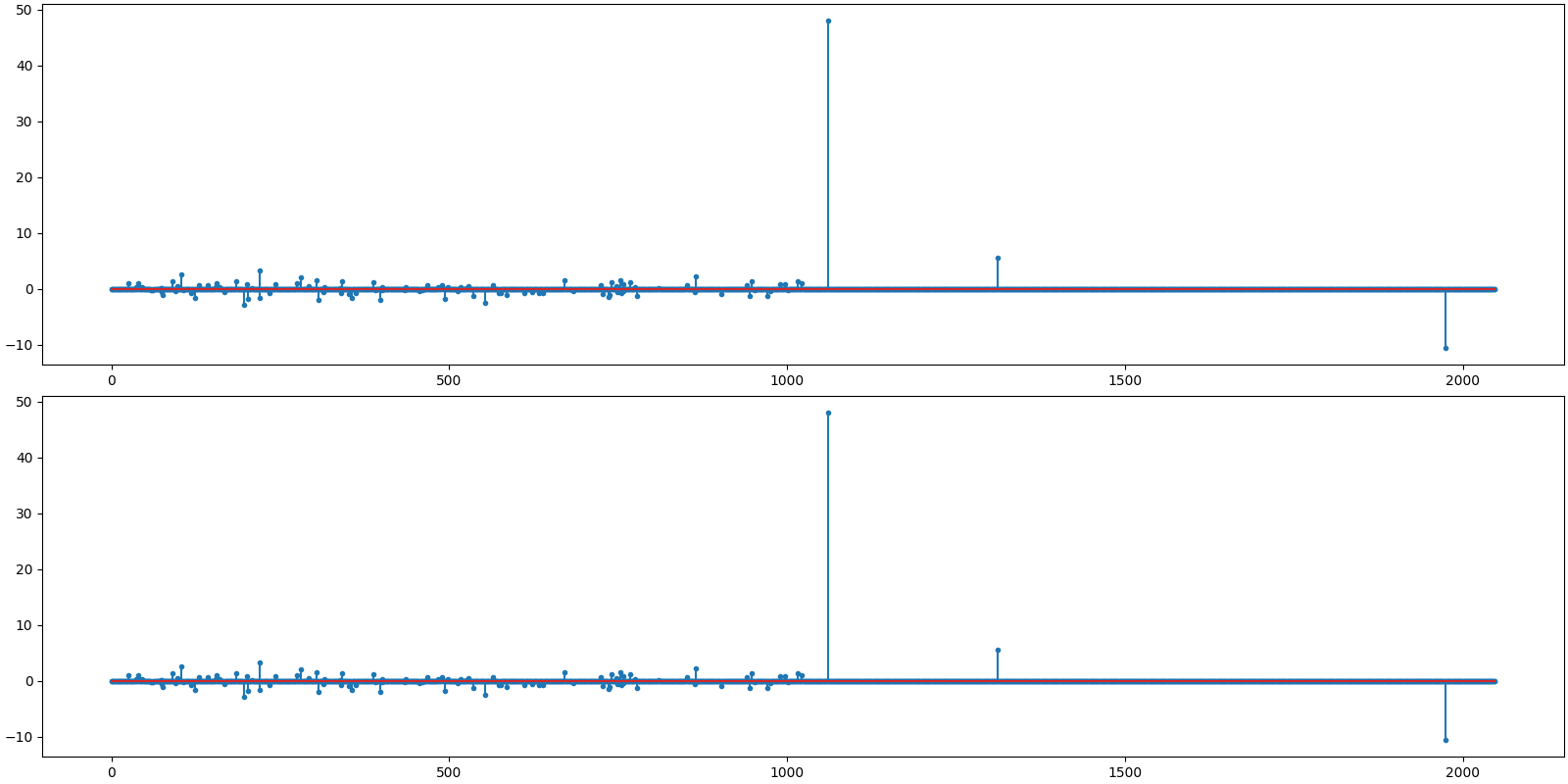
<StemContainer object of 3 artists>

Let us visualize the original and reconstructed signal

ax = crplot.h_plots(2)
ax[0].plot(b0)
ax[1].plot(b)

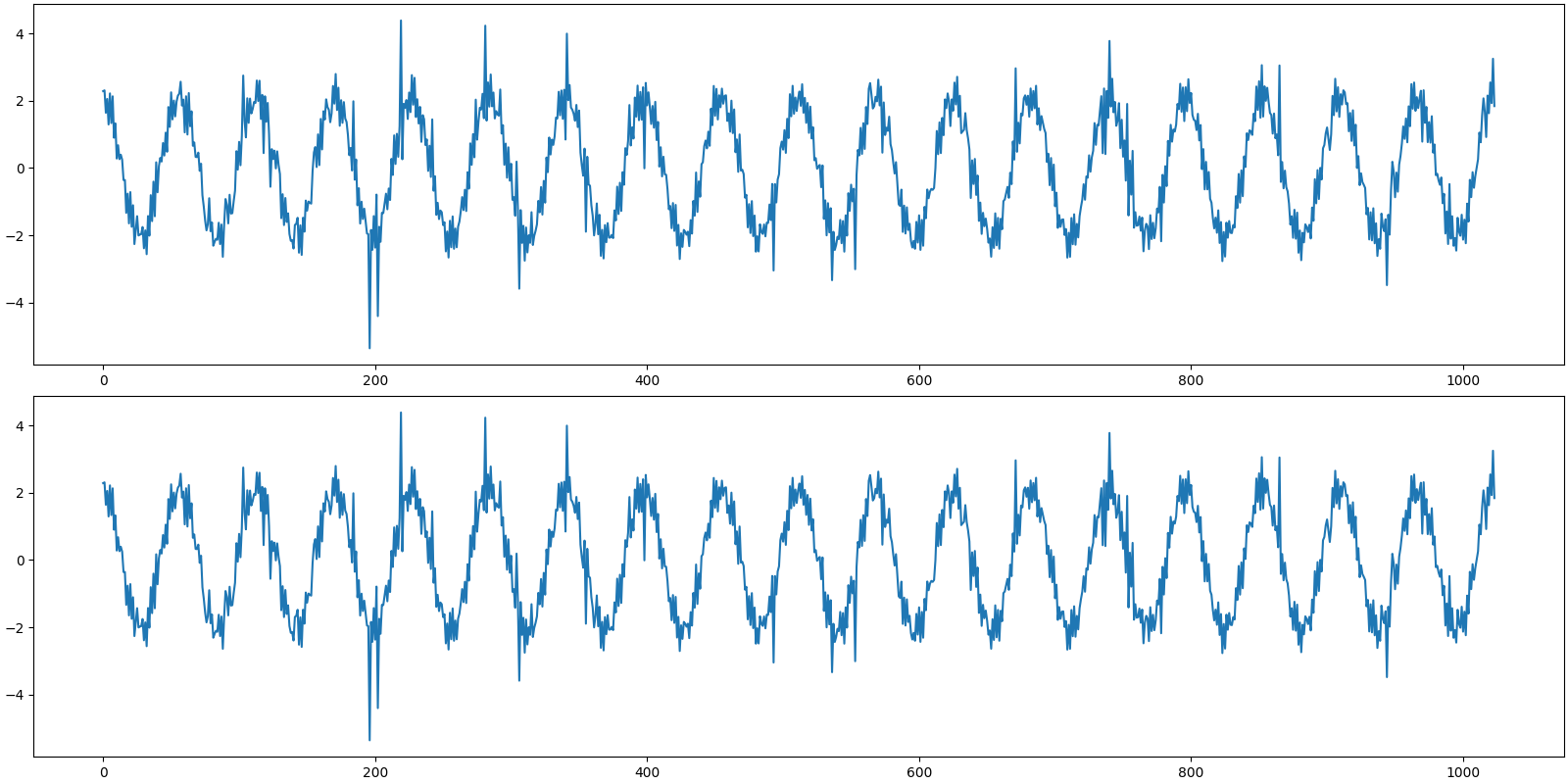
[<matplotlib.lines.Line2D object at 0x7f20052029d0>]

Sparse Recovery using SPGL1

import cr.sparse.cvx.spgl1 as crspgl1
options = crspgl1.SPGL1Options()
sol = crspgl1.solve_bp_jit(A, b0, options=options)
problems.analyze_solution(prob, sol, perc=100)

m: 1024, n: 2048
b_norm: original: 50.698 reconstruction: 50.698 SNR: 123.14 dB
x_norm: original: 50.704 reconstruction: 50.704 SNR: 115.88 dB
Sparsity: original: 123, reconstructed: 123, overlap: 123, ratio: 1.000
Iterations: 55 n_times: 58, n_trans: 56

The estimated sparse representation

x = sol.x

Let us reconstruct the signal from this sparse representation

b = prob.reconstruct(x)

Let us visualize the original and reconstructed representation

ax = crplot.h_plots(2)
ax[0].stem(x0, markerfmt='.')
ax[1].stem(x, markerfmt='.')

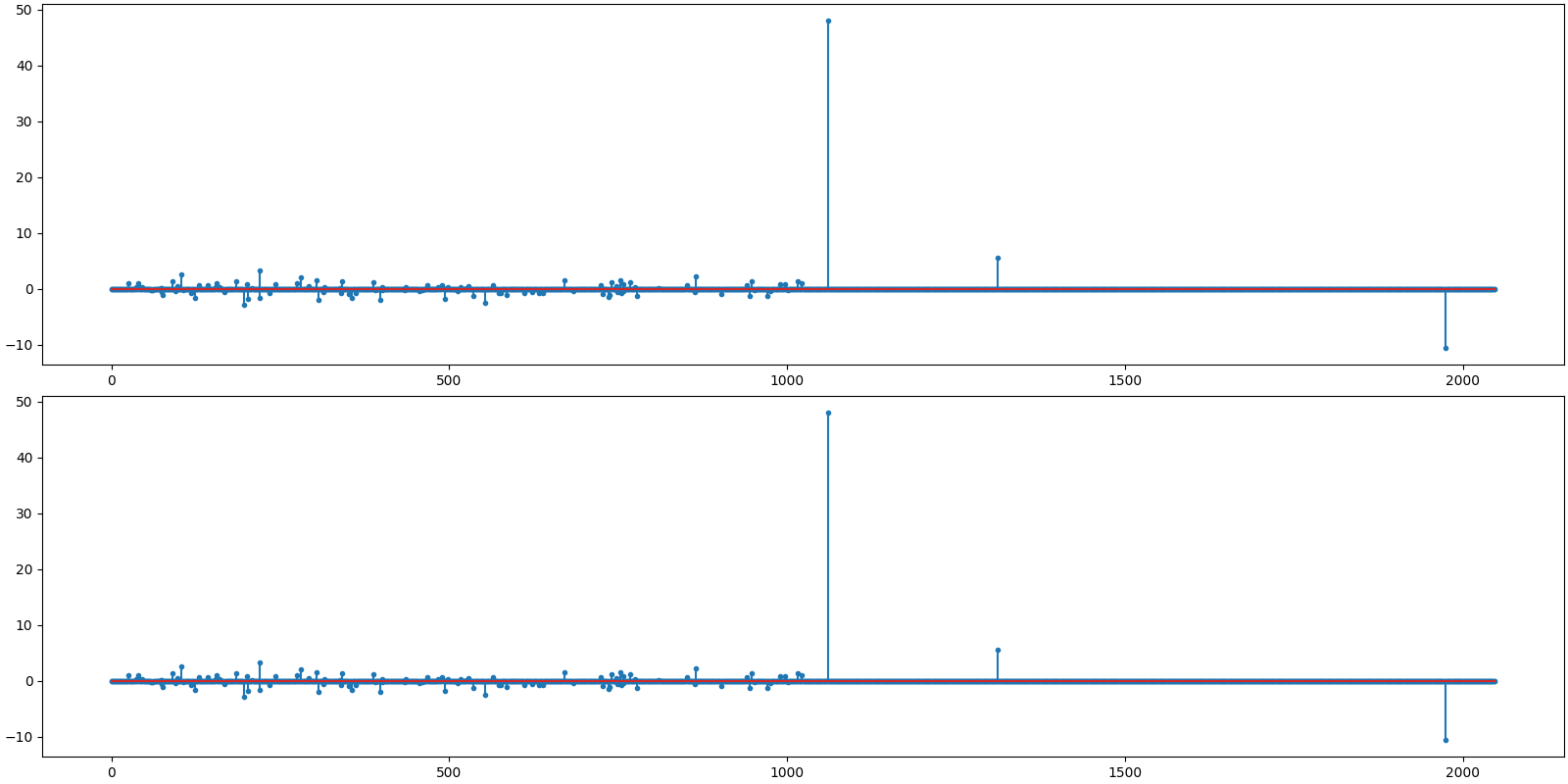
<StemContainer object of 3 artists>

Let us visualize the original and reconstructed signal

ax = crplot.h_plots(2)
ax[0].plot(b0)
ax[1].plot(b)

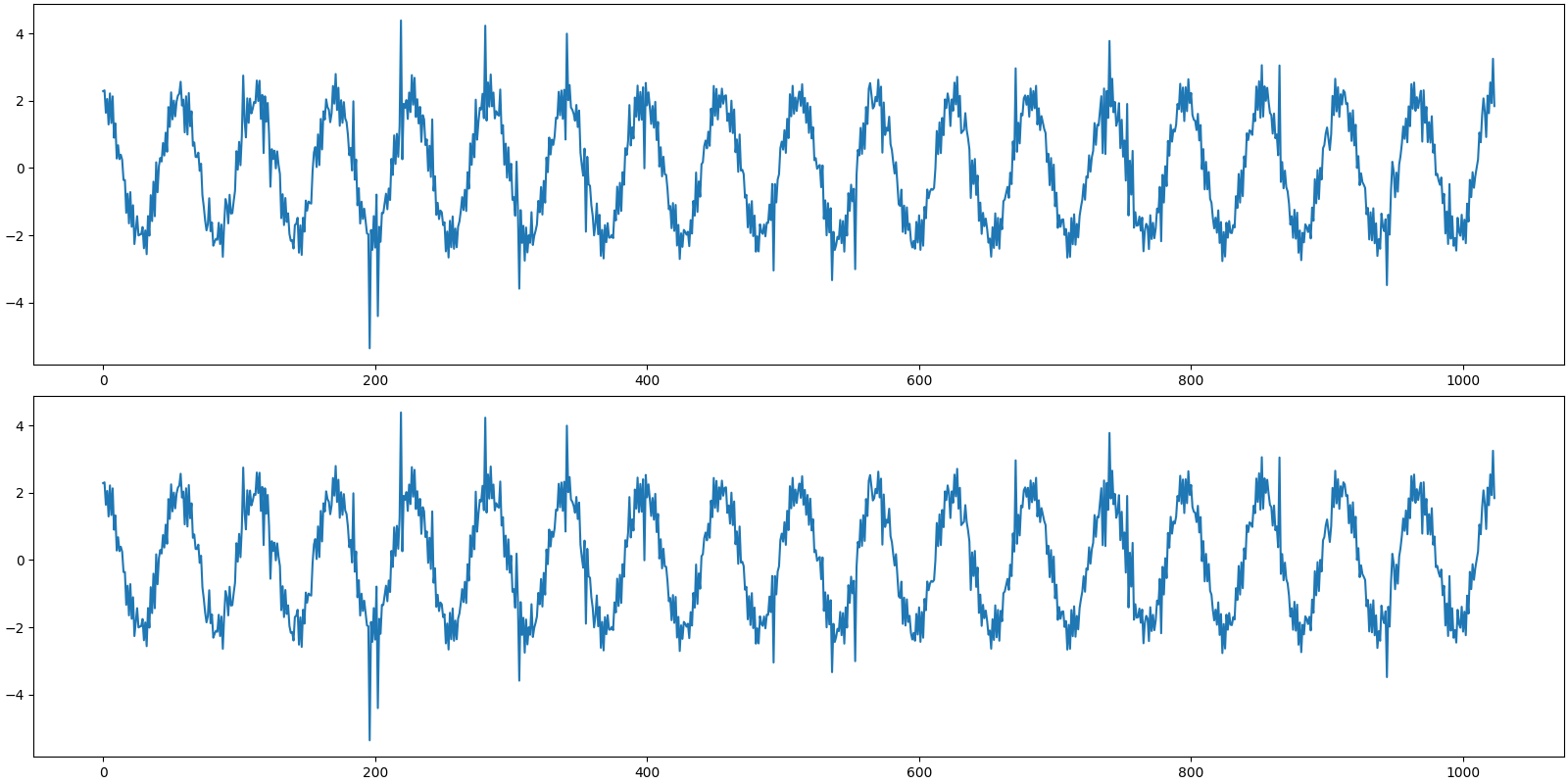
[<matplotlib.lines.Line2D object at 0x7f200ca71d90>]

Comments

• Both SP and CoSaMP correctly recover the signal in 5 iterations if the sparsity is specified properly.

• SP recovery is slightly inaccurate if the sparsity is incorrectly specified. It also takes more iterations to converge.

• SPGL1 converges in 55 iterations but correctly discovers the support.