1 bit Compressive Sensing

This example demonstrates following features - Making 1-bit quantized compressive measurements of a sparse signal - Recovering the original signal using the BIHT (Binary Iterative Hard Thresholding) algorithm.

Let’s import necessary libraries

import jax.numpy as jnp
from jax.numpy.linalg import norm

import matplotlib as mpl
import matplotlib.pyplot as plt

import cr.nimble as cnb
import cr.sparse as crs
import cr.sparse.dict as crdict
import cr.sparse.data as crdata
import cr.sparse.cs.cs1bit as cs1bit

from cr.nimble.dsp import (
    build_signal_from_indices_and_values
)

Setup

# Number of measurements
M = 256
# Ambient dimension
N = 512
# Sparsity level
K = 4

Sensing Matrix

Phi = crdict.gaussian_mtx(cnb.KEYS[0], M, N, normalize_atoms=False)
# frame bound
s0 = crdict.upper_frame_bound(Phi)
print(s0)
fig=plt.figure(figsize=(8,6), dpi= 100, facecolor='w', edgecolor='k')
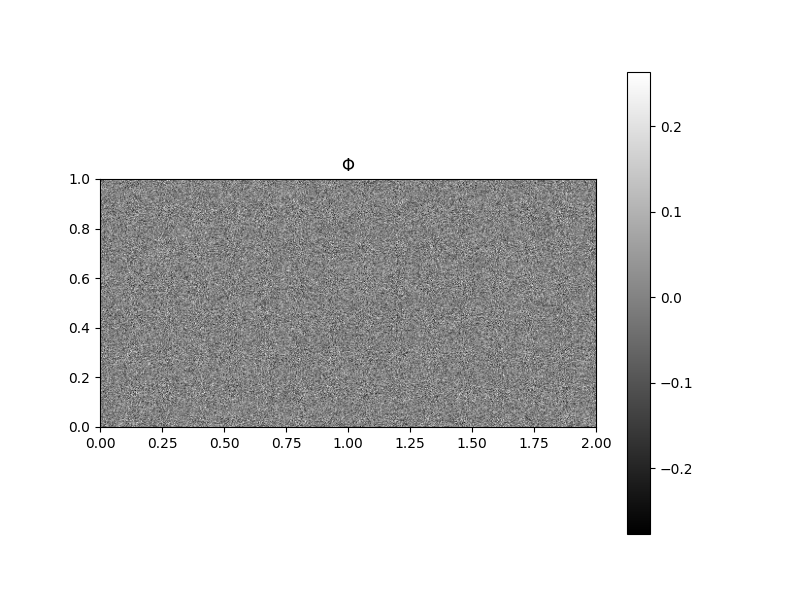
plt.imshow(Phi, extent=[0, 2, 0, 1])
plt.gray()
plt.colorbar()
plt.title(r'$\Phi$')

2.4003416483791433

Text(0.5, 1.0, '$\\Phi$')

K-sparse signal

x, omega = crdata.sparse_normal_representations(cnb.KEYS[1], N, K)
# normalize signal
x = x / norm(x)
# the support indices
print(omega)
fig=plt.figure(figsize=(8,6), dpi= 100, facecolor='w', edgecolor='k')
plt.stem(x, markerfmt='.')

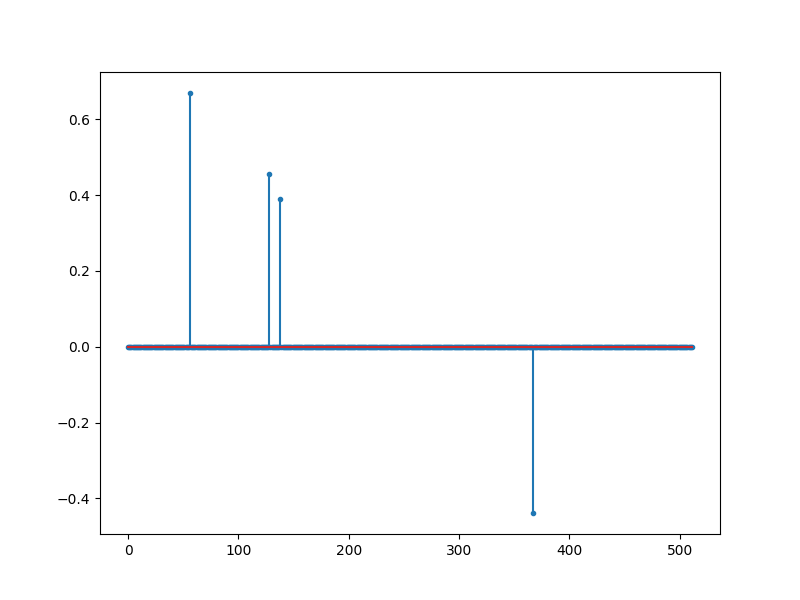
[ 56 128 138 367]

<StemContainer object of 3 artists>

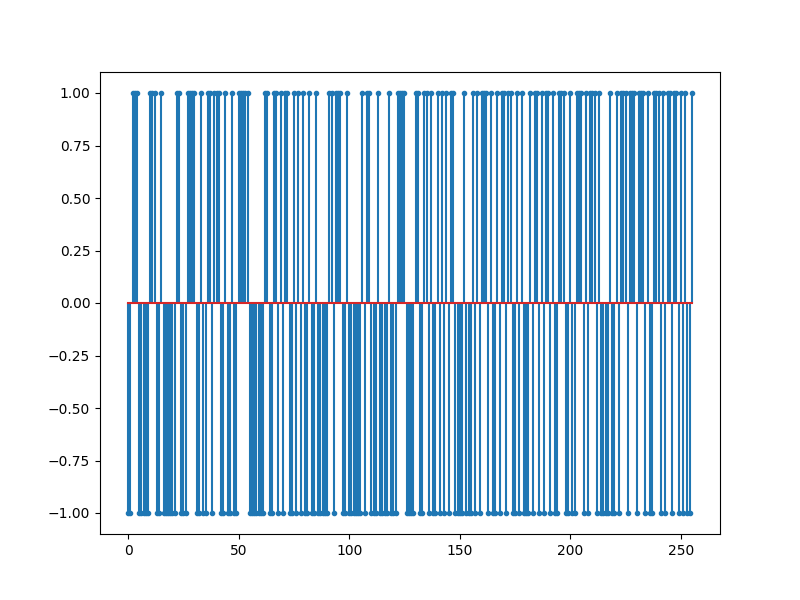
Measurement process

measurements

y = cs1bit.measure_1bit(Phi, x)
fig=plt.figure(figsize=(8,6), dpi= 100, facecolor='w', edgecolor='k')
plt.stem(y, markerfmt='.')
print(y)

[-1. -1.  1.  1.  1. -1. -1. -1. -1. -1.  1.  1.  1. -1. -1.  1. -1. -1.
 -1. -1. -1. -1.  1.  1. -1. -1. -1.  1.  1.  1.  1. -1. -1.  1. -1. -1.
  1.  1. -1.  1.  1.  1. -1. -1.  1. -1. -1.  1. -1. -1.  1.  1.  1.  1.
  1. -1. -1. -1. -1. -1. -1. -1.  1.  1. -1. -1.  1.  1. -1.  1. -1.  1.
  1. -1. -1.  1. -1.  1. -1.  1. -1. -1.  1. -1. -1.  1. -1. -1. -1. -1.
 -1.  1.  1. -1.  1.  1.  1. -1. -1.  1. -1. -1. -1. -1. -1. -1.  1. -1.
  1.  1. -1. -1. -1.  1. -1. -1. -1. -1.  1. -1. -1. -1.  1.  1.  1.  1.
 -1. -1. -1. -1.  1.  1. -1. -1.  1.  1. -1.  1. -1. -1.  1. -1.  1. -1.
  1. -1.  1.  1. -1. -1. -1. -1.  1. -1. -1. -1.  1. -1.  1. -1.  1.  1.
  1. -1.  1. -1. -1.  1. -1.  1.  1. -1.  1.  1. -1. -1.  1. -1.  1. -1.
 -1. -1.  1. -1.  1.  1. -1.  1. -1.  1.  1. -1.  1. -1. -1.  1.  1.  1.
 -1. -1.  1. -1. -1.  1.  1.  1. -1.  1. -1.  1.  1.  1. -1.  1. -1. -1.
 -1. -1.  1. -1. -1.  1. -1.  1.  1.  1. -1.  1.  1.  1. -1.  1.  1.  1.
 -1.  1. -1. -1.  1.  1.  1. -1.  1. -1.  1.  1. -1.  1.  1. -1.  1. -1.
  1. -1. -1.  1.]

Signal Reconstruction using BIHT

solver step-size

tau = 0.98 * s0
# solution
sol = cs1bit.biht_jit(Phi, y, K, tau)

reconstructed signal

x_rec = build_signal_from_indices_and_values(N, sol.I, sol.x_I)

Verification

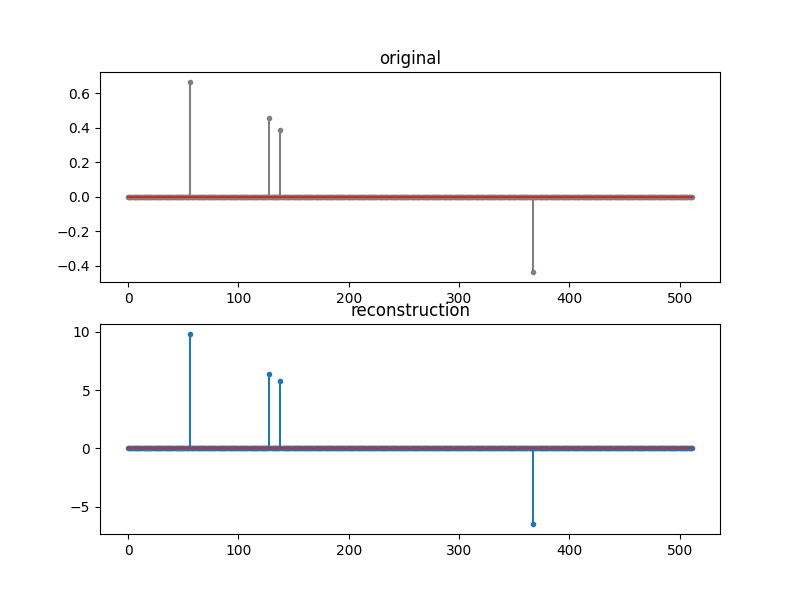
fig=plt.figure(figsize=(8,6), dpi= 100, facecolor='w', edgecolor='k')
plt.subplot(211)
plt.title('original')
plt.stem(x, markerfmt='.', linefmt='gray')
plt.subplot(212)
plt.stem(x_rec, markerfmt='.')
plt.title('reconstruction')

# recovered support
I = jnp.sort(sol.I)
print(I)

[ 56 128 138 367]

check if the support is recovered correctly

print(jnp.array_equal(omega, I))
# normalize recovered signal
x_rec = x_rec / norm(x_rec)
# the norm of error
print(norm(x - x_rec))

True
0.024352999672904573