FOcal Underdetermined System Solver (FOCUSS)

This is a simple example of using the FOcal Underdetermined System Solver (FOCUSS).

We can use the algorithm to solve a sparse recovery problem from compressive measurements.

# Configure JAX for 64-bit computing
from jax.config import config
config.update("jax_enable_x64", True)

Let’s import necessary libraries

import jax
import jax.numpy as jnp
import cr.nimble as crn
import cr.sparse as crs
import cr.sparse.pursuit.mp as mp
import cr.sparse.data as crdata
import cr.sparse.dict as crdict
import cr.sparse.plots as crplot
import cr.sparse.cvx.focuss as focuss

Problem setup

# Number of compressive measurements
m = 50
# Ambient dimension
n = 100
# Number of non-zero entries in the sparse model
k = 16

Gaussian sensing matrix

Phi = crdict.gaussian_mtx(crn.KEYS[0], m, n)

Spikes as sample data

x0, omega = crdata.sparse_spikes(crn.KEYS[1], n, k)

Compressive sensing/measurements

y = Phi @ x0

FOCUSS with p=1

p = 1.
iters = 6

FOCUSS step by step

ax = crplot.h_plots(iters+2, height=1)
ax[0].stem(x0, markerfmt='.')
# Initial guess for solution
x = jnp.ones(n)
ax[1].stem(x, markerfmt='.')
for i in range(iters):
    # Update solution [one step]
    x = focuss.step_noiseless(Phi, y, x, p=p)
    # Plot the updated solution
    ax[i+2].stem(x, markerfmt='.')

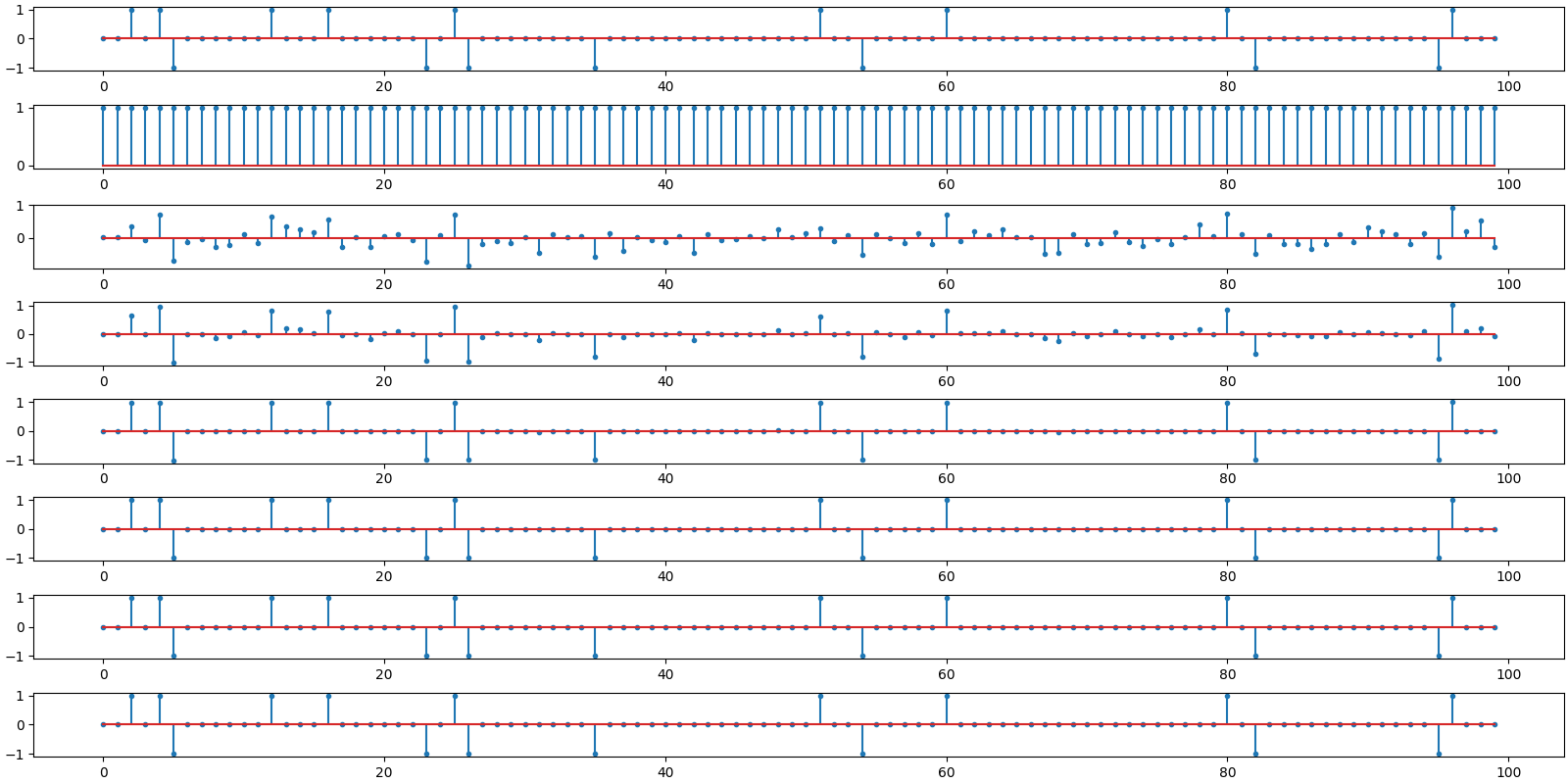
FOCUSS method full

sol = focuss.matrix_solve_noiseless(Phi, y, p=p, max_iters=10)
print(sol)
# solution vector
x_hat = sol.x

iterations=10
m=50, n=100, k=16
r_norm=6.892023e-15
x_norm=4.000000e+00

Metrics

snr = crn.signal_noise_ratio(x, x_hat)
prd = crn.percent_rms_diff(x, x_hat)
n_rmse = crn.normalized_root_mse(x, x_hat)
print(f'SNR: {snr:.2f} dB, PRD: {prd:.2f} %, N-RMSE: {n_rmse:.2e}')

SNR: 272.70 dB, PRD: 0.00 %, N-RMSE: 2.32e-14

Plot the solution

ax = crplot.h_plots(2, height=2)
ax[0].stem(x0, markerfmt='.')
ax[1].stem(x_hat, markerfmt='.')

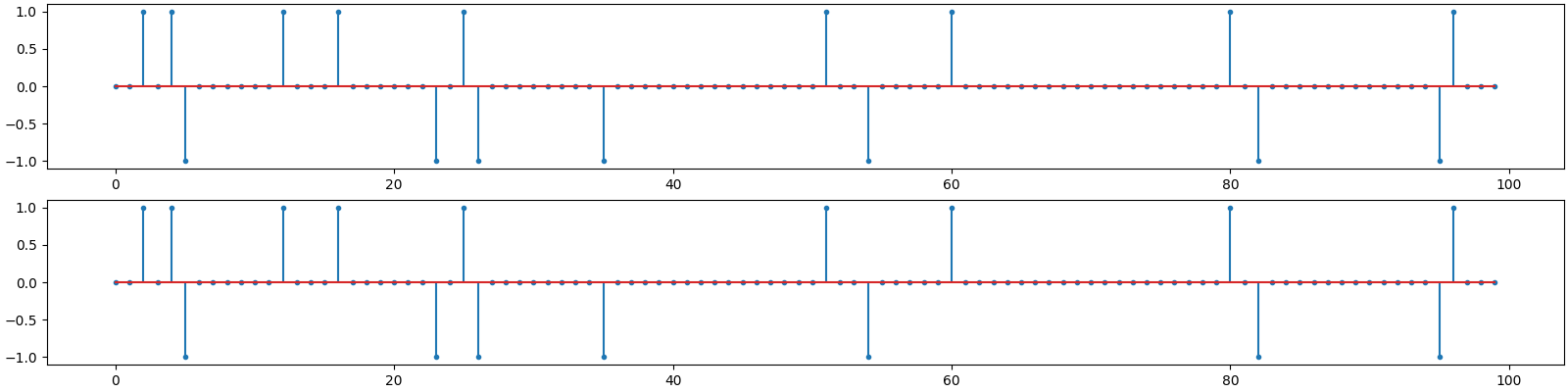
<StemContainer object of 3 artists>

FOCUSS with p=0.5

p = 0.5
iters = 9

FOCUSS step by step

ax = crplot.h_plots(iters+2, height=1)
ax[0].stem(x0, markerfmt='.')
# Initial guess for solution
x = jnp.ones(n)
ax[1].stem(x, markerfmt='.')
for i in range(iters):
    x = focuss.step_noiseless(Phi, y, x, p=p)
    ax[i+2].stem(x, markerfmt='.')

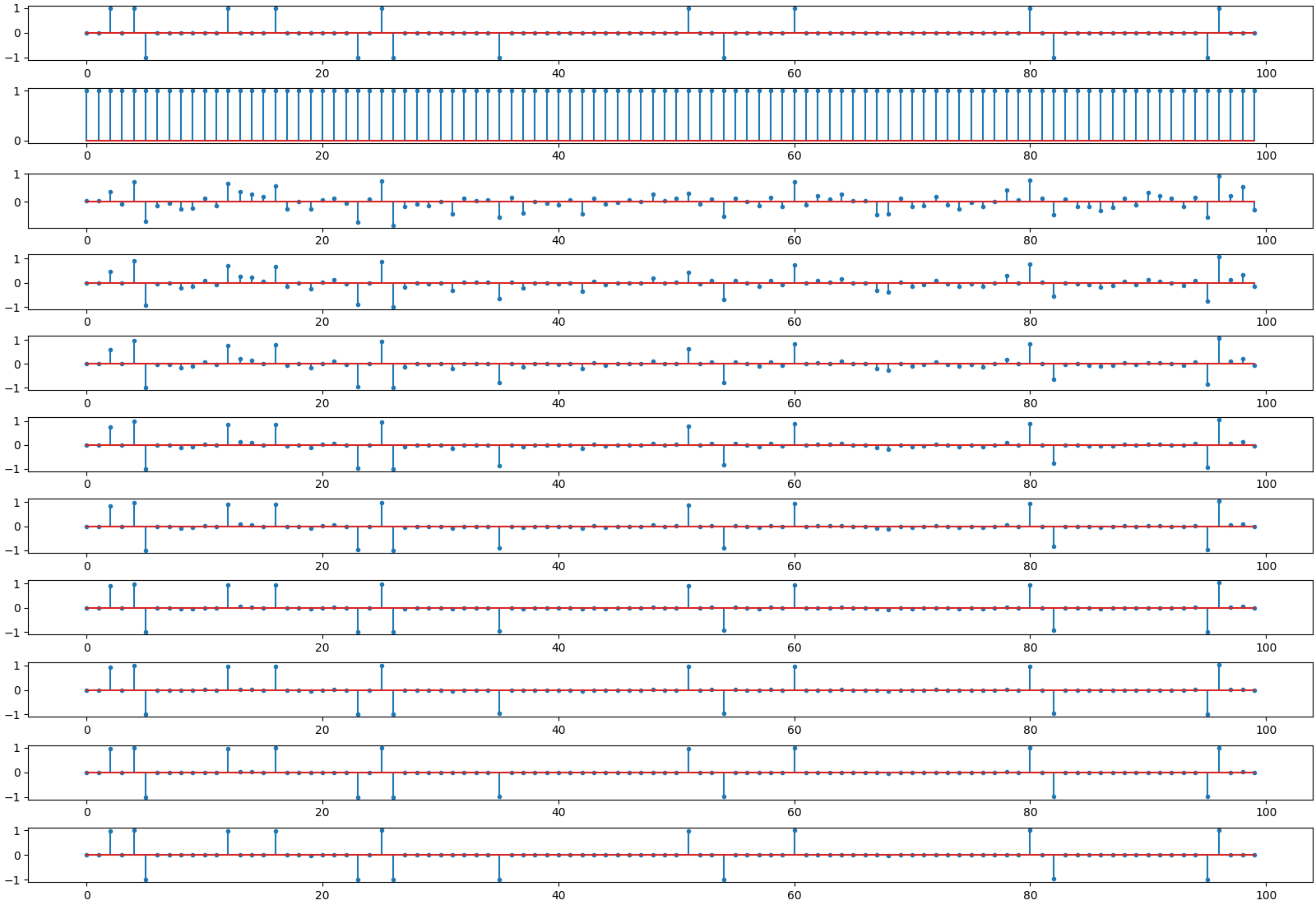
FOCUSS method full

sol = focuss.matrix_solve_noiseless(Phi, y, p=p, max_iters=10)
print(sol)
# solution vector
x_hat = sol.x

iterations=10
m=50, n=100, k=16
r_norm=2.088181e-15
x_norm=3.981269e+00

Metrics

snr = crn.signal_noise_ratio(x, x_hat)
prd = crn.percent_rms_diff(x, x_hat)
n_rmse = crn.normalized_root_mse(x, x_hat)
print(f'SNR: {snr:.2f} dB, PRD: {prd:.2f} %, N-RMSE: {n_rmse:.2e}')

SNR: 43.89 dB, PRD: 0.64 %, N-RMSE: 6.39e-03

Plot the solution

ax = crplot.h_plots(2, height=2)
ax[0].stem(x0, markerfmt='.')
ax[1].stem(sol.x, markerfmt='.')

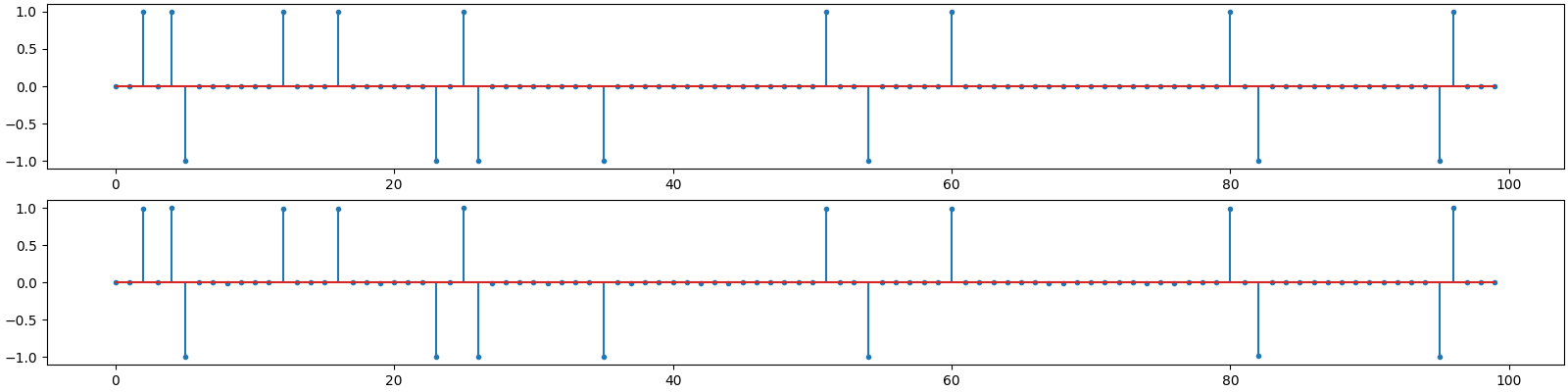
<StemContainer object of 3 artists>