Wavelet Transform Operators

This example demonstrates following features:

• cr.sparse.lop.convolve2D A 2D convolution linear operator

• cr.sparse.sls.lsqr LSQR algorithm for solving a least square problem on 2D images

Let’s import necessary libraries

import jax.numpy as jnp
# For plotting diagrams
import matplotlib.pyplot as plt
## CR-Sparse modules
import cr.nimble as cnb
# Linear operators
from cr.sparse import lop
# Sample images
import skimage.data
# Utilities
from cr.nimble.dsp import time_values
# Configure JAX for 64-bit computing
from jax.config import config
config.update("jax_enable_x64", True)

1D Wavelet Transform Operator

A signal consisting of multiple sinusoids

Individual sinusoids have different frequencies and amplitudes. Sampling frequency

fs = 1000.
# Time duration
T = 2
# time values
t = time_values(fs, T)
# Number of samples
n = t.size
x = jnp.zeros(n)
freqs = [25, 7, 9]
amps = [1, -3, .8]
for  (f, amp) in zip(freqs, amps):
    sinusoid = amp * jnp.sin(2 * jnp.pi * f * t)
    x = x + sinusoid
# Plot the signal
plt.figure(figsize=(8,2))
plt.plot(t, x, 'k', label='Composite signal')

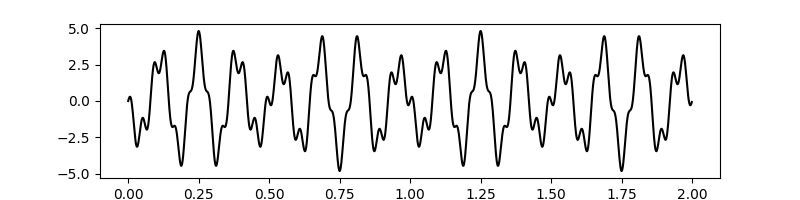
[<matplotlib.lines.Line2D object at 0x7f20292c1dc0>]

1D wavelet transform operator

DWT_op = lop.dwt(n, wavelet='dmey', level=5)

Wavelet coefficients

alpha = DWT_op.times(x)
plt.figure(figsize=(8,2))
plt.plot(alpha, label='Wavelet coefficients')

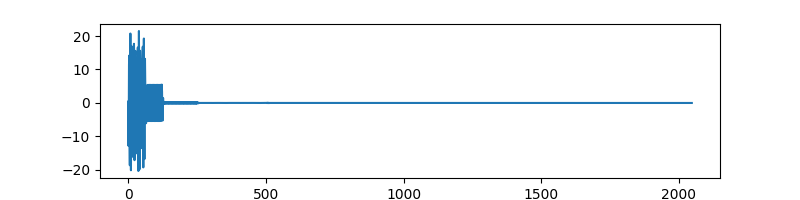
[<matplotlib.lines.Line2D object at 0x7f1ffe0846a0>]

Compression

Let’s keep only 10 percent of the coefficients

cutoff = n // 10
alpha2 = alpha.at[cutoff:].set(0)
plt.figure(figsize=(8,2))
plt.plot(alpha2, label='Wavelet coefficients after compression')

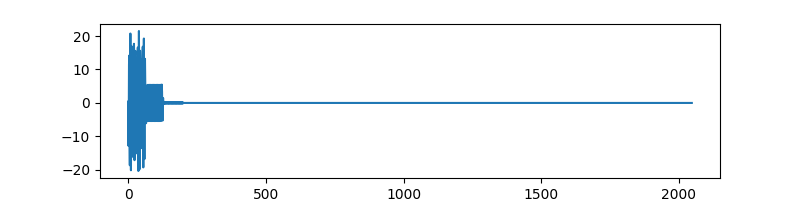
[<matplotlib.lines.Line2D object at 0x7f1ffc68cf70>]

Reconstruction

x_rec = DWT_op.trans(alpha2)
# RMSE
rmse = cnb.root_mse(x, x_rec)
print(rmse)
# SNR
snr = cnb.signal_noise_ratio(x, x_rec)
print(snr)
plt.figure(figsize=(8,2))
plt.plot(x, 'k', label='Original')
plt.plot(x_rec, 'r', label='Reconstructed')
plt.title('Reconstructed signal')
plt.legend()

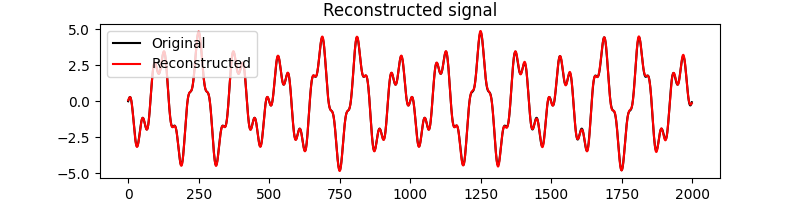
0.034259365997888466
36.56352988951201

<matplotlib.legend.Legend object at 0x7f2005f22490>

2D Wavelet Transform Operator

# Sample image
image = skimage.data.grass()
DWT2_op = lop.dwt2D(image.shape, wavelet='haar', level=5)
DWT2_op = lop.jit(DWT2_op)

Wavelet coefficients

coefs = DWT2_op.times(image)

Compression

Let’s keep only 1/16 of the coefficients

h, w = coefs.shape
coefs2 = jnp.zeros_like(coefs)
coefs2 = coefs2.at[:h//4, :w//4].set(coefs[:h//4, :w//4])

Reconstruction

image_rec = DWT2_op.trans(coefs2)
# RMSE
rmse = cnb.root_mse(image, image_rec)
print(rmse)
# PSNR
psnr = cnb.peak_signal_noise_ratio(image, image_rec)
print(psnr)

# Plot everything
fig, axs = plt.subplots(1, 4, figsize=(16, 3))
axs[0].imshow(image, cmap='gray')
axs[0].set_title('Image')
axs[0].axis('tight')

axs[1].imshow(coefs, cmap='gray_r', vmin=-1e2, vmax=1e2)
axs[1].set_title('DWT2 coefficients')
axs[1].axis('tight')

axs[2].imshow(coefs2, cmap='gray_r', vmin=-1e2, vmax=1e2)
axs[2].set_title('After compression')
axs[2].axis('tight')

axs[3].imshow(image_rec, cmap='gray')
axs[3].set_title('Reconstructed image')
axs[3].axis('tight')

27.383743287757877
19.380947312633058

(-0.5, 511.5, 511.5, -0.5)